Connecting host programs to adcc¶
Documentation for host programs and how to talk to adcc
Python dictionary or HDF5 file¶
-
class
adcc.DataHfProvider(data)¶ -
__init__(data)¶ Initialise the DataHfProvider class with the data being a supported data container (currently python dictionary or HDF5 file). Let nf denote the number of Fock spin orbitals (i.e. the sum of both the alpha and the beta orbitals) and nb the number of basis functions. With array we indicate either a np.array or an HDF5 dataset. The following keys are required in the container:
restricted (bool): True for a restricted SCF calculation, False otherwise
conv_tol (float): Tolerance value used for SCF convergence, should be roughly equivalent to l2 norm of the Pulay error.
orbcoeff_fb (.array with dtype float, size (nf, nb)): SCF orbital coefficients, i.e. the uniform transform from the basis to the molecular orbitals.
occupation_f (array with dtype float, size (nf, ): Occupation number for each SCF orbitals (i.e. diagonal of the HF density matrix in the SCF orbital basis).
orben_f (array with dtype float, size (nf, ): SCF orbital energies
fock_ff (array with dtype float, size (nf, nf): Fock matrix in SCF orbital basis. Notice, the full matrix is expected also for restricted calculations.
eri_phys_asym_ffff (array with dtype float, size (nf, nf, nf, nf): Antisymmetrised electron-repulsion integral tensor in the SCF orbital basis, using the Physicists’ indexing convention, i.e. that the index tuple (i,j,k,l) refers to the integral
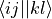 , i.e.
, i.e.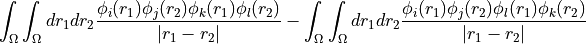
The full tensor (including zero blocks) is expected.
As an alternative to eri_phys_asym_ffff, the user may provide
eri_ffff (array with dtype float, size (nf, nf, nf, nf): Electron-repulsion integral tensor in chemists’ notation. The index tuple (i,j,k,l) thus refers to the integral
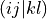 , which is
, which is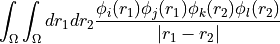
Notice, that no antisymmetrisation has been applied in this tensor.
The above keys define the least set of quantities to start a calculation in adcc. In order to have access to properties such as dipole moments or to get the correct state energies, further keys are highly recommended to be provided as well.
energy_scf (float): Final total SCF energy of both electronic and nuclear energy terms. (default: 0.0)
multipoles: Container with electric and nuclear multipole moments. Can be another dictionary or simply an HDF5 group.
elec_1 (array, size (3, nb, nb)): Electric dipole moment integrals in the atomic orbital basis (i.e. the discretisation basis with nb elements). First axis indicates cartesian component (x, y, z).
nuc_0 (float): Total nuclear charge
nuc_1 (array size (3, ): Nuclear dipole moment
The defaults for all entries are all-zero multipoles.
spin_multiplicity (int): The spin mulitplicity of the HF ground state described by the data. A value of 0 (for unknown) should be supplied for unrestricted calculations. (default: 1 for restricted and 0 for unrestricted calculations)
A descriptive string for the backend can be supplied optionally as well. In case of using a python dict as the data container, this should be done using the key backend. For an HDF5 file, this should be done using the attribute backend. Defaults based on the filename are generated.
- Parameters
data (dict or h5py.File) – Dictionary containing the HartreeFock data to use. For the required keys see details above.
-
Host-program specific interface¶
For implementing a host-program specific interface
to adcc, taking advantage of all features of the host program,
a derived class of the adcc.HartreeFockProvider has to be implemented.
The interface for this is:
-
class
adcc.HartreeFockProvider¶ Abstract class defining the interface for passing data from the host program to adcc. All functions of this class need to be overwritten explicitly from python. In the remaining documentation we denote with nf the value returned by get_n_orbs_alpha() and with nb the value returned by get_nbas().
-
fill_eri_ffff(self: libadcc.HartreeFockProvider, arg0: tuple, arg1: numpy.ndarray) → None¶ Fill the passed numpy array arg1 with a part of the electron-repulsion integral tensor in the molecular orbital basis. The indexing convention is the chemist’s notation, i.e. the index tuple (i,j,k,l) refers to the integral
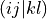 . The block to store is specified by the provided tuple of ranges arg0, which gives the range of indices to place into the buffer along each of the axis. The index counting is done in spin orbitals, so the full range in each axis is range(0, 2 * nf).
. The block to store is specified by the provided tuple of ranges arg0, which gives the range of indices to place into the buffer along each of the axis. The index counting is done in spin orbitals, so the full range in each axis is range(0, 2 * nf).
-
fill_eri_phys_asym_ffff(self: libadcc.HartreeFockProvider, arg0: tuple, arg1: numpy.ndarray) → None¶ Fill the passed numpy array arg1 with a part of the antisymmetrised electron-repulsion integral tensor in the molecular orbital basis. The indexing convention is the physicist’s notation, i.e. the index tuple (i,j,k,l) refers to the integral
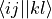 . The block to store is specified by the provided tuple of ranges arg0, which gives the range of indices to place into the buffer along each of the axis. The index counting is done in spin orbitals, so the full range in each axis is range(0, 2 * nf).
. The block to store is specified by the provided tuple of ranges arg0, which gives the range of indices to place into the buffer along each of the axis. The index counting is done in spin orbitals, so the full range in each axis is range(0, 2 * nf).
-
fill_fock_ff(self: libadcc.HartreeFockProvider, arg0: tuple, arg1: numpy.ndarray) → None¶ Fill the passed numpy array arg1 with a part of the Fock matrix in the molecular orbital basis. The block to store is specified by the provided tuple of ranges arg0, which gives the range of indices to place into the buffer along each of the axis. The index counting is done in spin orbitals, so the full range in each axis is range(0, 2 * nf). The implementation should not assume that the alpha-beta and beta-alpha blocks are not accessed even though they are zero by spin symmetry.
-
fill_occupation_f(self: libadcc.HartreeFockProvider, arg0: numpy.ndarray) → None¶ Fill the passed numpy array of size (2 * nf, ) with the occupation number for each SCF orbital.
-
fill_orbcoeff_fb(self: libadcc.HartreeFockProvider, arg0: numpy.ndarray) → None¶ Fill the passed numpy array of size (2 * nf, nb) with the SCF orbital coefficients, i.e. the uniform transform from the one-particle basis to the molecular orbitals.
-
fill_orben_f(self: libadcc.HartreeFockProvider, arg0: numpy.ndarray) → None¶ Fill the passed numpy array of size (2 * nf, ) with the SCF orbital energies.
-
flush_cache(self: libadcc.HartreeFockProvider) → None¶ This function is called to signal that potential cached data could now be flushed to save memory or other resources. This can be used to purge e.g. intermediates for the computation of electron-repulsion integral tensor data.
-
get_conv_tol(self: libadcc.HartreeFockProvider) → float¶ Returns the tolerance value used for SCF convergence. Should be roughly equivalent to the l2 norm of the Pulay error.
-
get_energy_scf(self: libadcc.HartreeFockProvider) → float¶ Returns the final total SCF energy (sum of electronic and nuclear terms.
-
get_n_bas(self: libadcc.HartreeFockProvider) → int¶ Returns the number of spatial one-electron basis functions. This value is abbreviated by nb in the documentation.
-
get_n_orbs_alpha(self: libadcc.HartreeFockProvider) → int¶ Returns the number of HF spin orbitals of alpha spin. It is assumed the same number of beta spin orbitals are used. This value is abbreviated by nf in the documentation.
-
get_nuclear_multipole(self: libadcc.HartreeFockProvider, arg0: int) → numpy.ndarray[numpy.float64]¶ Returns the nuclear multipole of the requested order. For 0 returns the total nuclear charge as an array of size 1, for 1 returns the nuclear dipole moment as an array of size 3.
-
get_restricted(self: libadcc.HartreeFockProvider) → bool¶ Return True for a restricted SCF calculation, False otherwise.
-
get_spin_multiplicity(self: libadcc.HartreeFockProvider) → int¶ Returns the spin multiplicity of the HF ground state. A value of 0* (for unknown) should be supplied for unrestricted calculations.
-
has_eri_phys_asym_ffff(self: libadcc.HartreeFockProvider) → bool¶ Returns whether fill_eri_phys_asym_ffff function is implemented and should be used(True) or whether antisymmetrisation should be done inside adcc starting from the fill_eri_ffff function (False)
-
Examples in the adcc source code for these interface are located in the adcc/backend folder. For example pyscf.py or psi4.py.
Note
TODO Explain the OperatorIntegralProvider and its mechanism.
C++ interface¶
For directly passing data to libadcc on the C++ level, the following interface needs to be implemented:
-
class
libadcc::HartreeFockSolution_i¶ Access to a Hartree-Fock solution where all quantities are available in the MO orbital basis.
This is the interface an SCF code needs to supply in order to be useful for libadcc.
To explain the index ordering, we will refer to a calculation with six basis functions, labelled from b1 to b6 and four spatial molecular orbitals. In order of increasing energy these will be labelled 1a to 4a for the orbitals with alpha spin and 1b to 4b the orbitals with beta spin. We take n_alpha == 2 and n_beta == 2, such that 1a, 2a, 1b and 2b are occupied and the others are virtual.
In general b indices run over the basis functions, i.e. [b1, b2, …, b6] and f indices over the mos, blocked by alpha and beta, i.e. [1a, 2a, 3a, 4a, 1b, 2b, 3b, 4b].
System information
-
void
nuclear_multipole(size_t order, scalar_type *buffer, size_t size) const = 0¶ Fill a buffer with nuclear multipole data for the nuclear multipole of given order.
Sizes of the data
-
size_t
n_orbs_alpha() const = 0¶ Return the number of HF spin molecular orbitals of alpha spin. It is assumed the same number of beta spin orbitals are obtained. In our example: 4
-
size_t
n_orbs() const¶ Return the total number of computed HF spin molecular orbitals
- Note
equals n_alpha_orbs() + n_beta_orbs()
-
size_t
n_bas() const = 0¶ Return the number of spatial one electron basis functions
In our example: 6
Access to HF SCF results
-
std::string
backend() const = 0¶ Provide access to a descriptive string, which identifies the implementation / SCF program used to provide the data
-
bool
restricted() const = 0¶ Was the HF algorithm a restricted HF
If this is true adcc will assume that the alpha and beta values of certain quantities (like the MO coefficients) are exactly identical.
-
size_t
spin_multiplicity() const = 0¶ What is the spin multiplicity of the reference state represented by this class.
A special value of 0 indicates that the spin is not known or an unrestricted calculation was employed
-
void
orbcoeff_fb(scalar_type *buffer, size_t size) const = 0¶ Fill a buffer with the HF molecular orbital coefficients.
After the function call the buffer contains the coefficient matrix as a full n_orbs() times n_bas() block in row-major ordering.
The indexing convention for f and b is as explained above, i.e. the first index runs like [1a 2a 3a 4a 1b 2b 3b 4b] and the second like [b1 b2 b3 b4 b5 b6] in the example explained above.
- Parameters
buffer: The pointer into the memory to fillsize: The maximal number of elements the buffer pointer is valid for.
-
void
orben_f(scalar_type *buffer, size_t size) const = 0¶ Fill a buffer with the HF molecular orbital energies ordered increasing in energy but blocked by alpha and beta, i.e. in our example we have [1a 2a 3a 4a 1b 2b 3b 4b].
After the function call the buffer contains the energies as a full n_orbs() block.
- Parameters
buffer: The pointer into the memory to fillsize: The maximal number of elements the buffer pointer is valid for.
-
void
occupation_f(scalar_type *buffer, size_t size) const = 0¶ Occupation numbers of each of the spin orbitals. Only the values 1.0 and 0.0 at each of the entries are supported. After the function call the buffer contains the occupation numbers as a full n_orbs() block.
In our example: [1.0 1.0 1.0 1.0 0.0 0.0 1.0 1.0 1.0 1.0 0.0 0.0]
- Parameters
buffer: The pointer into the memory to fillsize: The maximal number of elements the buffer pointer is valid for.
Access to quantities in an MO basis
-
void
fock_ff(size_t d1_start, size_t d1_end, size_t d2_start, size_t d2_end, size_t d1_stride, size_t d2_stride, scalar_type *buffer, size_t size) const = 0¶ Fill a buffer with a block of the fock matrix elements in the MO basis.
The block to access is specified by the means of half-open ranges in each of the two index dimensions as [
d1_start,d1_end) as well as [d2_start,d2_end`).The ordering is such that the
n_orbs_alpha()orbitals of alpha spin go first in each of the dimensions followed by then_orbs_alpha()beta orbitals. Otherwise the ordering should be identical to the one oforbital_energies_f()andcoeff_fb(). I.e. in our examplefruns like [1a 2a 3a 4a 1b 2b 3b 4b] in both dimensions.The buffer is used to return the computed values. The storage format is determined by d1_stride and d2_stride, which define the strides to be used to write data in each dimension.
The theoretical full fock matrix which could be returned is hence of size n_orbs() times n_orbs(). The implementation should not assume that the alpha-beta and beta-alpha blocks are not accessed even though they are zero by spin symmetry.
- Note
For a canonical basis this thing is diagonal with the orbital energies, but for non-canonical ADC it might not be the case.
-
void
eri_ffff(size_t d1_start, size_t d1_end, size_t d2_start, size_t d2_end, size_t d3_start, size_t d3_end, size_t d4_start, size_t d4_end, size_t d1_stride, size_t d2_stride, size_t d3_stride, size_t d4_stride, scalar_type *buffer, size_t size) const = 0¶ Fill a buffer with a block of the two electron repulsion integrals in the MO basis.
The block is specified by the means of half-open ranges in each of the four indices using the parameters
d1_start,d1_end,d2_start,d2_end,d3_start,d3_end,d4_start,d4_end, for examplestd::vector<double> buffer; hf.repulsion_integrals_ffff(0,5, 0,5, 0,5, 0,5, buffer.data());
will return the block of integrals running from indices 0-4 in each of the indices, i.e. a buffer of 5^4 = 625 entries.
Within each dimension the ordering is assumed to be the same as
orbital_energies_f()andcoeff_fb(), i.e. then_orbs_alpha()orbitals of alpha spin go first, followed by then_orbs_alpha()beta orbitals. I.e. in our examplefruns like [1a 2a 3a 4a 1b 2b 3b 4b] in both dimensions.The buffer is used to return the computed values. The storage format is determined by d1_stride to d3_stride, which define the strides to be used to write data in each dimension.
- Note
The convention used for the indexing in this function is chemist’s notation or shell-pair notation, i.e. if
(ij|kl)is the element (i,j,k,l) of the buffer, then this describes the integralsuch that orbital indices i/j and k/l are on the same centre.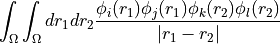
- Note
If
has_eri_phys_asym_ffff()is true, this function is never called directly and may implemented only as a dummy.
-
void
eri_phys_asym_ffff(size_t d1_start, size_t d1_end, size_t d2_start, size_t d2_end, size_t d3_start, size_t d3_end, size_t d4_start, size_t d4_end, size_t d1_stride, size_t d2_stride, size_t d3_stride, size_t d4_stride, scalar_type *buffer, size_t size) const = 0¶ Fill a buffer with a block of the antisymmetrised two electron repulsion integrals in the MO basis using the physicist’s indexing convention.
This function works similar to
repulsion_integrals_ffffbut returns the anti-symmetrised integrals in physicist’s notation instead. In other words if <ij||kl> is the term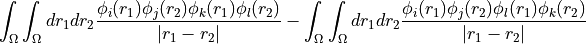
- Note
If
has_eri_phys_asym_ffff()is false, this function is never called directly and may implemented only as a dummy.
-
bool
has_eri_phys_asym_ffff() const¶ Has the eri_phys_asym_ffff function been implemented and is available
-
void
flush_cache() const¶ Tell the implementation side, that potentially cached data could now be flushed to save memory or other resources. This can be used to purge e.g. intermediates for the computation of eri tensor data.
-
~HartreeFockSolution_i()¶ Virtual desctructor
-
void