DictHfProvider

class adcc.DictHfProvider(*args, **kwargs)

Bases: adcc.DataHfProvider.DataHfProvider

Initialise the DataHfProvider class with the data being a supported data container (currently python dictionary or HDF5 file). Let nf denote the number of Fock spin orbitals (i.e. the sum of both the alpha and the beta orbitals) and nb the number of basis functions. With array we indicate either a np.array or an HDF5 dataset. The following keys are required in the container:

  1. restricted (bool): True for a restricted SCF calculation, False otherwise

  2. conv_tol (float): Tolerance value used for SCF convergence, should be roughly equivalent to l2 norm of the Pulay error.

  3. orbcoeff_fb (.array with dtype float, size (nf, nb)): SCF orbital coefficients, i.e. the uniform transform from the basis to the molecular orbitals.

  4. occupation_f (array with dtype float, size (nf, ): Occupation number for each SCF orbitals (i.e. diagonal of the HF density matrix in the SCF orbital basis).

  5. orben_f (array with dtype float, size (nf, ): SCF orbital energies

  6. fock_ff (array with dtype float, size (nf, nf): Fock matrix in SCF orbital basis. Notice, the full matrix is expected also for restricted calculations.

  7. eri_phys_asym_ffff (array with dtype float, size (nf, nf, nf, nf): Antisymmetrised electron-repulsion integral tensor in the SCF orbital basis, using the Physicists’ indexing convention, i.e. that the index tuple (i,j,k,l) refers to the integral 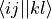\langle ij || kl \rangle, i.e.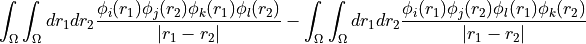

    \int_\Omega \int_\Omega d r_1 d r_2 \frac{ \phi_i(r_1) \phi_j(r_2) \phi_k(r_1) \phi_l(r_2)}{|r_1 - r_2|} - \int_\Omega \int_\Omega d r_1 d r_2 \frac{ \phi_i(r_1) \phi_j(r_2) \phi_l(r_1) \phi_k(r_2)}{|r_1 - r_2|}

    The full tensor (including zero blocks) is expected.

As an alternative to eri_phys_asym_ffff, the user may provide

  1. eri_ffff (array with dtype float, size (nf, nf, nf, nf): Electron-repulsion integral tensor in chemists’ notation. The index tuple (i,j,k,l) thus refers to the integral 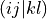(ij|kl), which is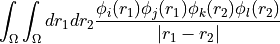

    \int_\Omega \int_\Omega d r_1 d r_2 \frac{\phi_i(r_1) \phi_j(r_1) \phi_k(r_2) \phi_l(r_2)}{|r_1 - r_2|}

    Notice, that no antisymmetrisation has been applied in this tensor.

The above keys define the least set of quantities to start a calculation in adcc. In order to have access to properties such as dipole moments or to get the correct state energies, further keys are highly recommended to be provided as well.

  1. energy_scf (float): Final total SCF energy of both electronic and nuclear energy terms. (default: 0.0)

  2. multipoles: Container with electric and nuclear multipole moments. Can be another dictionary or simply an HDF5 group.

    • elec_1 (array, size (3, nb, nb)): Electric dipole moment integrals in the atomic orbital basis (i.e. the discretisation basis with nb elements). First axis indicates cartesian component (x, y, z).

    • nuc_0 (float): Total nuclear charge

    • nuc_1 (array size (3, ): Nuclear dipole moment

    The defaults for all entries are all-zero multipoles.

  3. spin_multiplicity (int): The spin mulitplicity of the HF ground state described by the data. A value of 0 (for unknown) should be supplied for unrestricted calculations. (default: 1 for restricted and 0 for unrestricted calculations)

A descriptive string for the backend can be supplied optionally as well. In case of using a python dict as the data container, this should be done using the key backend. For an HDF5 file, this should be done using the attribute backend. Defaults based on the filename are generated.

Parameters

data (dict or h5py.File) – Dictionary containing the HartreeFock data to use. For the required keys see details above.